Materi Himpunan Kelas 7 SMP dan Contoh Soal – Hallo guys, selamat buat kalian yang saat ini sudah berada di kelas 7 SMP yah. Tentunya menjadi semakin bersemangat juga bukan untuk mempelajari materi – materi pelajaran yang mungkin sebelumnya sudah pernah di perkenalkan
ketika masih duduk di bangku SD. Di materi yang akan kita ulas kali ini tentang himpunan. Secara umum himpunan diartikan sebagai perkumpulan atau segerombolan. Misalnya sekumpulan iibu-ibu disebut juga dengan himpunan ibu – ibu.
Saat kalian ke pasar, kalian akan melihat banyak jenis dagangan yang dijajakan dengan jenis yang seragam dikelompokkan di tempat yang sama. seperti kelompok penjual sayuran, ada kelompok pedagang buah, dan kelompok pedagang ikan, dan lainnya. Hal ini disebut himpunan
Lalu bagaimana himpunan dalam materi matematika? langsung saja kalian baca artikelnya sampai habis dan pastikan kalian berdoa terlebih dahulu supaya lancar dalam memahami materi yang akan dibahas nantinya.

Ulasan Materi Himpunan Kelas 7 SMP
Pengertian Dasar Himpunan
Konsep himpunan pertama kali ditemukan oleh ahli ilmu matematika berkewarganegaraan Jerman di abad ke 18, yang bernama George Cantor (1845 – 1918). Dari definisi di atas, dapat disimpulkan bahwa yang dimaksud dengan objek yang telah terdefinisi dengan jelas adalah suatu benda yang sudah jelas wujudnya, seperti boneka, binatang, angka, warna, dan lain-lain.
Contoh kumpulan objek himpunan adalah:
1. Siswa-siswa kelas VII A,
2. Kelompok angka 2, 4, 5, 8,
3. Kumpulan siswa SMP Bahtera yang mengikuti latihan menari,
4. Jenis-jenis hewan pemakan daging.
Contoh di atas adalah himpunan sebab objek-objeknya telah terdefinisi dengan jelas. Kumpulan benda atau objek belum tentu merupakan suatu himpunan.
Konsep Himpunan
Di dalam kehidupan sehari-hari, kata himpunan ini dipadankan dengan kumpulan, kelompok, grup, atau gerombolan. Dalam biologi misalnya, kita mengenal kelompok flora dan kelompok fauna. Di dalamnya, masih ada lagi kelompok vertebrata, kelompok invertebrata, kelompok dikotil, dan kelompok monokotil.
Dalam kehidupan sehari-hari, kalian juga mengenal suku Jawa, suku Madura, suku Sasak, suku Dayak, suku Batak, dan lain-lain. Semua itu merupakan kelompok. Istilah kelompok, kumpulan, kelas, maupun gerombolan dalam matematika dikenal dengan istilah himpunan. Namun, tidak semua kumpulan termasuk himpunan. Contohnya kumpulan siswa yang pandai, kumpulan siswa yang berbadan tinggi.
Kumpulan yang termasuk bukan himpunan:
1. Kumpulan kota-kota bersih di Indonesia
2. Kumpulan orang miskin di Indonesia
3. Kumpulan murid yang pintar di sekolah
4. Kumpulan gunung tertinggi di Indonesia
5. Kumpulan mata pelajaran yang digemari siswa
6. Kumpulan makanan yang enak
Cara Penyajian Himpunan
Cara 1: Dinyatakan dengan menyebutkan anggotanya (enumerasi)
Suatu himpunan dapat dinyatakan dengan menyebutkan semua anggotanya yang dituliskan dalam kurung kurawal. Manakala banyak anggotanya sangat banyak, cara mendaftarkan ini biasanya dimodifikasi, yaitu diberi tanda tiga titik (“…”) dengan pengertian “dan seterusnya mengikuti pola”.
A = {3, 5, 7}
B = {2, 3, 5, 7}
C = {a, i, u, e, o}
D = {…, −3, −2, −1, 0, 1, 2, 3, …}
Cara 2: Dinyatakan dengan menuliskan sifat yang dimiliki anggotanya
Suatu himpunan dapat dinyatakan dengan menyebutkan sifat yang dimiliki anggotanya.
A adalah himpunan semua bilangan ganjil yang lebih dari 1 dan kurang dari 8.
B adalah himpunan semua bilangan prima yang kurang dari 10.
C adalah himpunan semua huruf vokal dalam abjad Latin.
D adalah himpunan bilangan bulat.
Sebelum kalian menyajikan himpunan dengan notasi pembentuk himpunan, sebaiknya kalian mengetahui dulu tentang himpunan bilangan dalam matematika sebagai berikut:
1. Himpunan semua bilangan asli dinotasikan A. Anggota A = {1, 2, 3, 4, …}
2. Himpunan semua bilangan cacah dinotasikan C. Anggota C = {0, 1, 2, 3, 4, …}
3. Himpunan semua bilangan bulat dinotasikan B. Anggota B = {…, −3, −2, −1, 0, 1, 2, 3, …}
4. Himpunan semua bilangan real dinotasikan R. Contoh bilangan Real: √3 , 2/3 , 3/4 , 0,45
Cara 3: Dinyatakan dengan notasi pembentuk himpunan
Suatu himpunan dapat dinyatakan dengan menuliskan syarat keanggotaan himpunan tersebut. Notasi ini biasanya berbentuk umum {x | P(x)} dimana x mewakili anggota dari himpunan, dan P(x) menyatakan syarat yang harus dipenuhi oleh x agar bisa menjadi anggota himpunan tersebut. Simbol x bisa diganti oleh variabel yang lain, seperti y, z, dan lain-lain. Misalnya A = {1, 2, 3, 4, 5} bisa dinyatakan dengan notasi pembentuk himpunan A = {x | x < 6, dan x ∈ asli}.
Lambang {x | x < 6, dan x ∈ asli} ini bisa dibaca sebagai “Himpunan x sedemikian sehingga x kurang dari 6 dan x adalah elemen bilangan asli}. Tetapi, jika kita sudah memahami dengan baik, maka lambang ini biasanya cukup dibaca dengan “Himpunan bilangan asli kurang dari 6”.

Diagram Venn
Cara menyajikan himpunan juga bisa dinyatakan dengan gambar atau diagram yang disebut dengan Diagram Venn. Diagram Venn diperkenalkan oleh pakar matematika Inggris bernama John Venn (1834 – 1923). Petunjuk dalam membuat diagram Venn antara lain:
1. Himpunan semesta (S) digambarkan sebagai persegi panjang dan huruf S diletakkan di sudut kiri atas.
2. Setiap himpunan yang ada dalam himpunan semesta ditunjukkan oleh kurva tertutup sederhana.
3. Setiap anggota himpunan ditunjukkan dengan titik.
4. Bila anggota suatu himpunan mempunyai banyak anggota, maka anggotaanggotanya tidak perlu dituliskan.
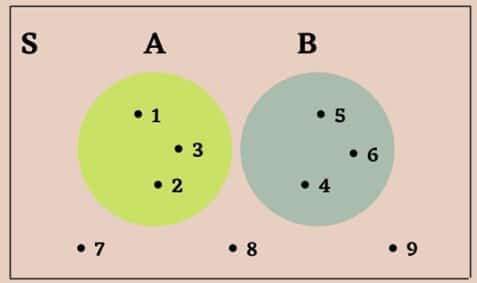
Amati contoh penyajian diagram venn di bawah ini!
Diagram Venn dari himpunan S ={1, 2, 3, 4, 5, 6, 7, 8, 9}, himpunan A = {1, 2, 3} dan himpunan B ={ 4, 5, 6} adalah sebagai berikut:
Baiklah adik-adik semua, itulah tadi ulasan lengkap mengenai materi himpunan semoga bisa kalian pahami dengan baik ya. Terimakasih sudah meluangkan waktu untuk membacanya dan buat ayah bunda terus dukung anak-anak kita supaya rajin belajar.
Karena dengan rajin belajar akan menjadi kunci kesuksesan mereka nantinya. Untuk menemukan materi pembelajaran lain dari SD sampai ke perguruan tinggi bisa di cari di kolom pencarian yah sampai jumpa di artikel lainnya.