Mengenal Gerak Harmonik Sederhana, Fisika Kelas 10

gerak harmonik sederhana – Saat tidur atau beristirahat di kasur kita pasti merasa nyaman berbaring diatas kasur yang empuk Nah sekarang ini banyak sekali orang yang menggunakan springbed untuk memperoleh kenyamanan saat tidur,

tahukah teman-teman kenyamanan tersebut diperoleh dari getaran pegas di dalam springbed yang dicampur dengan spons saat kita menaiki springbed maka pegas akan bergerak naik turun melewati titik setimbangnya dan dalam waktu tertentu pegas akan berhenti pada posisi atau keadaan semula.

Prinsip kerja pada pegas springbed merupakan aplikasi getaran harmonik yang sangat dekat dengan kita, jadi di artikel kali ini kita akan pelajari adalah gerak / getaran harmonik sederhana :

Materi Gerak Harmonik Sederhana Kelas 10

---

Apa Itu Getaran Harmonik ?

Tahukah teman-teman Apa itu getaran harmonik getaran harmonik adalah gerak bolak-balik benda menuju titik kesetimbangan dan terjadi secara terus-menerus jadi getaran harmonik dihasilkan oleh gaya yang menyebabkan benda bergetar dan selalu menuju kedudukan setimbang ya contoh getaran harmonik adalah getaran pada bandul atau ayunan dan getaran pada pegas

Terdapat beberapa persamaan pada getaran harmonik pertama persamaan simpangan simpangan getaran harmonik sederhana dirumuskan sebagai berikut y = a sin theta = a sin Omega t benda menghasilkan 1 getaran atau satu fase jika sudut yang ditempuh sebesar 2 phi Radian atau 360 derajat.

Persamaan Getaran Harmonik

Apabila benda telah menempuh sudut fase sebesar Teta 0 pada saat t = 0 maka persamaan simpangan menjadi y = a sin Omega t + Teta 0 besarnya Omega = 2 PF = 2 phi t dengan y adalah simpangan satuannya meter a amplitudo atau simpangan terjauh juga dalam m Omega kecepatan sudut dalam radian per sekon t waktu satuannya sekon Teta = Omega t + Teta 0 adalah sudut fase sudut fase awal keduanya dalam satuan radian, Frekuensi satuannya = Hz dan T = periode dalam sekon

Persamaan kedua adalah persamaan kecepatan kecepatan getaran harmonik adalah turunan pertama dari fungsi simpangan terhadap waktu v = d y per DX = d a sin Omega t + Teta 0 sehingga diperoleh P = Omega a cos Omega t + Teta 0 kecepatan maksimum terjadi ketika nilai cos Omega t + Teta 0 = 1 dengan demikian kecepatan maksimum getaran harmonik dirumuskan tema sama dengan Omega dengan v adalah kecepatan dan V Max merupakan kecepatan maksimum keduanya dalam satuan meter/sekon

Selanjutnya persamaan percepatan percepatan getaran harmonik adalah turunan pertama dari fungsi kecepatan terhadap waktu a = d = d Omega a cos Omega t + Teta 0 sehingga A = min Omega kuadrat Sin Omega t + Teta 0

Percepatan maksimum terjadi ketika nilai Sin Omega t + Teta 0 = 1 A = min Omega A kuadrat, A adalah percepatan dan amax percepatan maksimum keduanya dalam satuan meter per sekon kuadrat

Adapun hubungan kecepatan amplitudo dan simpangan ditunjukkan oleh persamaan V = Omega akar A kuadrat kurang y kuadrat dengan v adalah kecepatan getaran harmonik satuannya meter per sekon kecepatan sudut satuannya Radian per sekon a amplitudo dalam m dan Y merupakan simpangan dalam satuan meter

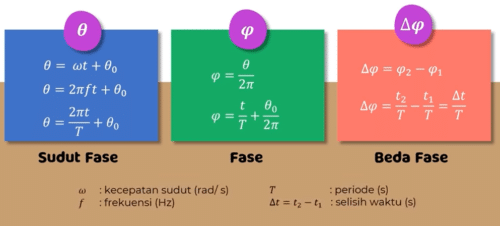
Sudut Fase, Fase, Dan Beda Fase (Getaran Harmonik)

Selanjutnya kita mengetahui sudut fase fase dan beda fase dalam getaran Jika sebuah benda bergetar harmonis dan membentuk sudut tertentu maka sudut tersebut disebut dengan sudut fase sudut fase dibagi sudut satu putaran disebut fase getaran sedangkan selisih 2 fase getaran disebut beda fase.

Berikut ini persamaan untuk menentukan sudut fase fase dan beda fase getaran sudut fase dirumuskan dengan Teta = Omega t + Teta 0 = 2 p f t + Teta 0 = 2 phi t + Teta 0 fase getaran dituliskan dalam persamaan V = Teta per 2 phi = t + Teta 0 per 2 phi dan beda fase dirumuskan dengan Delta v = v 2 Kurang 1 dan V = T 2 t kurang t 1 = Delta t Oke teman-teman itulah persamaan-persamaan pada getaran harmonik.

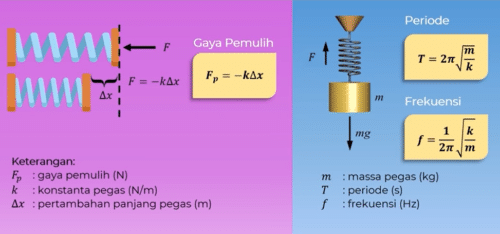
Getaran Harmonik Pada Pegas

Selanjutnya kita akan membahas getaran harmonik pada pegas dan bandul pertama getaran harmonik pada pegas sebuah pegas yang diberikan gaya akan cenderung kembali ke posisinya semula gaya yang menyebabkan pegas kembali ke posisinya semula Inilah yang disebut gaya pemulih besarnya gaya pemulih pada pegas

dituliskan dalam persamaan F = Min k Delta x f merupakan gaya pemulih satuannya Newton K adalah konstanta pegas dalam Newton per meter dan Delta X pertambahan panjang pegas dalam satuan m besarnya periode dan frekuensi pegas dapat dihitung dengan rumus T = 2 phi akar m karena F = 1 per t maka F = 1/2 phi akar k m dengan m massa pegas dalam kg D periode pegas satuannya sekon dan frekuensi pegas satuannya Hz

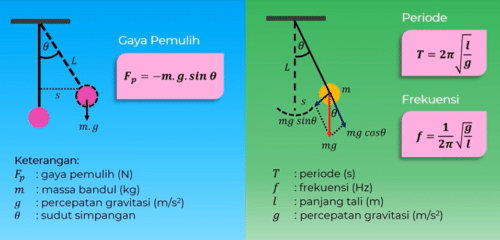
Getaran Harmonik Pada Bandul

Berikutnya getaran harmonik pada bandul besarnya gaya pemulih pada bandul dirumuskan dengan F P = Min MG Sin Teta f p gaya pemulih satuannya Newton m massa bandul dalam kg G percepatan gravitasi dalam satuan meter per sekon kuadrat dan Teta sudut simpangan

Periode pada bandul dihitung dengan rumus T = 2 phi akar l pergi dan frekuensi F = 1 per 2 phi akar g per l dengan l panjang tali dalam meter

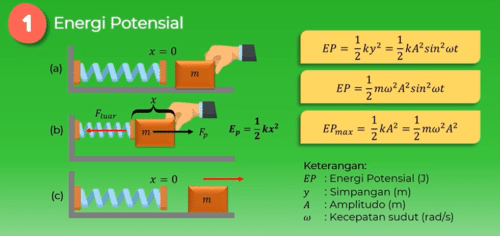
Energi Getaran Harmonik

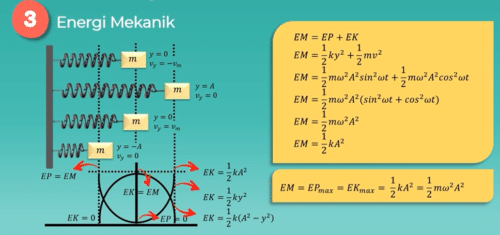
Benda yang bergerak harmonik akan memiliki energi potensial energi kinetik dan jumlah dari kedua energi tersebut yaitu energi mekanik energi potensial getaran harmonik dirumuskan dengan fx = setengah x kuadrat = setengah x kuadrat Sin kuadrat Omega T = setengah m kuadrat a kuadrat Sin kuadrat Omega t saat Sin kuadrat Omega t = 1 energi potensial maksimum dan dituliskan dalam rumus fx = setengah x kuadrat = setengah m Omega kuadrat a kuadrat.

Sedangkan energi kinetiknya dihitung dengan rumus p k = setengah MV kuadrat = setengah m kuadrat a kuadrat kurang y kuadrat = setengah K2 drat kurang y kuadrat energi kinetik maksimum diperoleh ketika benda berada pada titik setimbangnya atau y = 0 dan dituliskan dalam persamaan X = setengah Kak kuadrat = setengah m kuadrat a kuadrat

Dan energi mekanik pada getaran harmonik dirumuskan sebagai berikut m = x + x = setengah x kuadrat + setengah MV kuadrat setengah x kuadrat = setengah m kuadrat a kuadrat Sin kuadrat Omega t dan setengah MV kuadrat = setengah m kuadrat a kuadrat cos kuadrat Omega t jika kita jabarkan diperoleh m = setengah m kuadrat a kuadrat = setengah K2 drat dari persamaan tersebut energi mekanik yang terjadi pada benda yang bergetar harmonik tidak bergantung pada waktu dan tempat sehingga energi mekanik yang terjadi pada benda di manapun berada adalah sama m = f x = x = setengah K2 drat atau sama juga dengan setengah Omega kuadrat a kuadrat nah sampai di sini teman-teman bisa paham ya

Oke jadi itu saja ya temen-temen ulasan seputar getaran harmonik sederhana yang sudah kami jabarkan secara lengkap, semoga mudah di mengerti dan di pahami ya, sukses selalu, salam : by : Prakerja.Co.Id