Materi Matematika Kelas 8 SMP Persamaan Garis Lurus

Materi Matematika Kelas 8 SMP Persamaan Garis Lurus – Hai adik-adik apa kabar kalian? semoga dalam keadaan sehat selalu ya. Di edisi kali ini kita akan memberilan ulasan materi pelajaran kelas 8 SMP tentang persamaan garis lurus. Apakah kalian sudah pernah mengenal materi ini?

Untuk dunia konstruksi bangunan, posisi dari bangunan tentunya menjadi hal yang paling utama yang harus diperhatikan. Bahkan, tingkat kemiringan bangunan tidak bisa diabaikan karena bisa mempengaruhi pada tingkat kekuatannya.

Dari pada banyak berbasa – basi lagi langsung saja kita bahas materi selengkapnya disini mulai dari Definisi, Rumus dan contoh soalnya. Jadi pastikan kalian membaca artikel ini sampao habis yah guys. Terima kasih banyak.

Ulasan Materi Persamaan Garis Lurus

Pengertian Persamaan Garis Lurus

Persamaan garis lurus adalah persamaan yang memuat satu atau lebih variabel, di mana masing-masing variabelnya berpangkat satu. Jika persamaan tersebut dilukiskan dalam diagram Cartesius, akan terbentuk grafik garis lurus dengan kemiringan tertentu. Kemiringan itu biasa disebut gradien garis (m).

Bentuk Persamaan Garis

Secara umum, persamaan garis lurus memiliki dua bentuk yaitu sebagai berikut.

1. Bentuk eksplisit

Bentuk eksplisit adalah bentuk persamaan garis yang memenuhi y = mx + c, dengan m = gradien garis dan c = konstanta.

Adapun contoh bentuk eksplisit adalah y = 3x + 6. Berdasarkan persamaan tersebut, gradien garisnya = 3.

2. Bentuk implisit

Bentuk implisit adalah bentuk persamaan garis yang memenuhi Ax + By + c = 0. Adapun contoh bentuk implisit adalah 3x – y + 6 = 0.

Berdasarkan persamaan tersebut, rumus gradien garis bisa dinyatakan sebagai

Jika digambarkan dalam diagram Cartesius, grafik persamaan garis lurus y = 3x + 6 atau 3x – y + 6 = 0 adalah sebagai berikut.

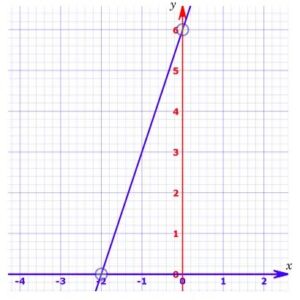
Cara Mencari Gradien

Sebelum mencari persamaan garis, Quipperian harus tahu dulu cara menentukan gradien garisnya. Inilah beberapa cara untuk menentukan gradien garis.

1. Gradien garis yang melalui dua titik

Jika sebuah garis lurus melalui dua titik koordinat A(x1,y1) dan B(x2,y2), maka gradiennya merupakan hasil bagi antara selisih nilai ordinat dan absisnya.

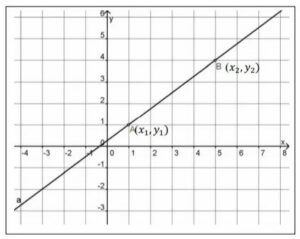
Secara matematis, dirumuskan sebagai berikut.

Perhatikan contoh berikut.

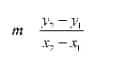
Tentukan gradien garis yang melalui titik A(-3,2) dan B(-2,5)!

Pembahasan

Tentukan dahulu nilai (x1,y1) dan (x2,y2)nya.

x1 = -3
y1 = 2
x2 = -2
y2 = 5

Untuk menentukan gradien garisnya, gunakan persamaan berikut.

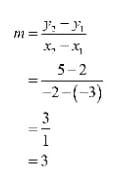
Jadi, gradien garisnya adalah 3.

2. Gradien tegak lurus

Jika dua garis saling tegak lurus, maka hasil kali gradien kedua garis tersebut sama dengan -1.

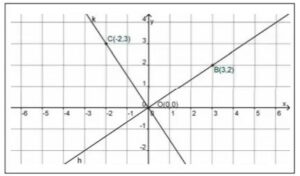
Mari kita buktikan!

Gradien garis k

Gradien garis h

Hubungan antara gradien garis k dan garis h adalah

Dengan demikian, terbukti bahwa hasil kali gradien kedua garis tersebut adalah -1. Secara matematis, rumus gradien tegak lurus dirumuskan sebagai berikut.

Dengan:

m1 = gradien garis ke-1; dan

m2 = gradien garis ke-2.

3. Gradien garis yang saling sejajar

Jika dua garis sama-sama sejajar, maka gradien kedua garis tersebut sama.

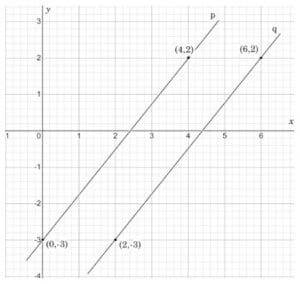
Mari kita buktikan!

Gradien garis p

Gradien garis q

Berdasarkan perhitungan, terbukti bahwa gradien garis p dan q adalah sama. Secara matematis, rumus gradien garis yang saling sejajar adalah sebagai berikut.

m1 = m2

Cara Mencari Persamaan Garis

Setelah sebelumnya Quipperian belajar bagaimana cara menentukan gradien garis, kini saatnya belajar bagaimana sih cara mencari persamaan garis itu. Ada beberapa cara untuk mencarinya, yaitu sebagai berikut.

1. Persamaan garis lurus melalui titik (x1,y1) dan bergradien m

Jika sebuah garis yang bergradien m melalui titik (x1,y1), rumus persamaan garis lurusnya adalah sebagai berikut.

Perhatikan contoh berikut.

Tentukan persamaan garis lurus yang melalui titik (6,-2) dan bergradien 2.

Pembahasan

Adapun nilai x1 = 6 dan y1 = -2, m = 2.

Dengan demikian, persamaan garis lurusnya adalah sebagai berikut.

Jadi, persamaan garisnya adalah y = 2x – 10.

2. Persamaan garis lurus melalui 2 titik, yaitu A(x1,y1) dan B(x2,y2)

Jika sebuah garis lurus melalui 2 titik A(x1,y1) dan B(x2,y2), maka persamaan garisnya ditentukan dengan rumus berikut.

Baiklah adik-adik itulah tadi ulasan materi mengenai Materi Matematika Kelas 8 SMP Persamaan Garis Lurus. Semoga kalian bisa memahami materi ini dengan baik sehingga nantinya bisa menjawab semua soal – soal yang berkaitan nantinya.