Gerak Melingkar, Fisika Kelas 10

prakerja.co.id : kali ini kami akan berbagi ilmu pengetahuan fisika khusus untuk kelas 10, dengan tema gerak melingkar ya, nah temen-temen ada yang sudah paham belum ?, apa itu gerak melingkar, oke kita akan bahas bersama di artikel ini ya.

Pernahkah teman-teman bermain ke taman hiburan di sana teman-teman bakal menemukan wahana permainan yang beragam dan salah satu mainan populer di taman hiburan adalah bianglala tahukah teman-teman bahwa prinsip kerja bianglala sangat erat hubungannya dengan konsep fisika yaitu gerak melingkar.

Table of Contents

Apa Itu Gerak Melingkar ?

Gerak melingkar adalah Gerak suatu benda menempuh lintasan melingkar dengan kecepatan tertentu benda lain yang juga menerapkan konsep gerak melingkar adalah kipas angin yang sedang menyala jarum jam yang bergerak dan komedi putar,

Besaran Gerak Melingkar

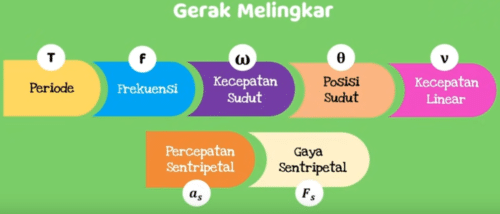
Sebelum kita membahas persamaan dalam gerak melingkar kita perlu ketahui besaran-besaran dalam gerak melingkar pertama periode dilambangkan dengan t berikutnya frekuensi simbolnya F kecepatan sudut lambangnya Omega posisi sudut ditandai dengan Teta kecepatan linier simbolnya V selanjutnya percepatan sentripetal atau atas dan terakhir gaya sentripetal atau FS

contoh gambar besaran gerak melingkar

Nah teman-teman sekarang kita bahas satu per satu Besaran dalam gerak melingkar yang pertama periode periode merupakan waktu yang diperlukan untuk melakukan satu putaran penuh periode dapat ditentukan dengan rumus t = t per besaran yang kedua frekuensi yang merupakan banyak putaran tiap satuan waktu frekuensi dapat dihitung menggunakan persamaan f = n t dengan t adalah waktu yang satuannya sekon dan n adalah banyak putaran

Hubungan Periode Dan Frekuensi

Adapun hubungan antara periode dan frekuensi adalah T = 1 F atau F = 1 t adalah simbol periode satuannya sekon dan F lambang dari frekuensi satuannya besaran berikutnya adalah posisi sudut yaitu besar sudut yang ditempuh tiap satuan waktu rumus untuk menentukan besarnya posisi sudut adalah Teta = Omega T = 2 phi F T = 2 phi t + teta merupakan posisi sudut dalam radian Omega adalah kecepatan sudut satuannya Radian per sekon dan t waktu satuannya sekon

Besaran selanjutnya adalah kecepatan sudut kecepatan sudut merupakan besar sudut yang ditempuh tiap satuan waktu kecepatan sudut dihitung dengan rumus Omega = 2 PF atau 2 phi t Omega adalah kecepatan sudut satuannya Radian per sekon frekuensi dalam hz dan periode satuannya sekon

kemudian kecepatan linear kecepatan linier adalah kecepatan benda untuk mengelilingi lingkaran arah kecepatan linier selalu menyinggung Sisi lingkaran kecepatan linear v = 2 phi r atau b = 2 phi r t = Omega Omega R dengan v adalah kecepatan linier satuannya meter per sekon Omega kecepatan sudut dalam radian per sekon dan R adalah jari-jari lingkaran satuannya meter

Lalu ada besaran percepatan sentripetal percepatan sentripetal disebabkan oleh adanya gaya yang selalu menuju pusat lingkaran rumus percepatan sentripetal adalah a s = v kuadrat R = Omega kuadrat R adalah percepatan sentripetal satuannya meter per sekon kuadrat c merupakan kecepatan linier satuannya meter Omega kecepatan sudut dalam satuan radian per sekon dan besaran yang terakhir adalah gaya sentripetal yaitu gaya yang arahnya selalu menuju pusat lingkaran dan tegak lurus dengan vektor kecepatan linier

Gaya sentripetal ditentukan dengan menggunakan persamaan f = m s = MV kuadrat R = M3 kuadrat r f s adalah gaya sentripetal satuannya Newton m adalah massa benda dalam kg as percepatan sentripetal dalam meter per sekon kuadrat

contoh gambar percepatan sentripetal dan gaya sentripetal

Analogi Dan Hubungan GLBB & GMBB

Gerak melingkar merupakan jenis gerak yang mirip namun tidak sama dengan gerak lurus perbedaannya terdapat pada jenis lintasannya jika pada gerak lurus terdapat gerak lurus berubah beraturan atau GLBB maka pada gerak melingkar juga terdapat gerak melingkar berubah beraturan atau GLBB besaran pada kedua gerak ini memiliki hubungan yaitu kecepatan linier sama dengan kecepatan sudut kali jari-jari percepatan linier sama dengan percepatan sudut X jari-jari dan posisi sama dengan posisi sudut X jari-jari sampai disini bisa dipahami ya

contoh gambar Analogi Dan Hubungan GLBB & GMBB

Gerak Melingkar Beraturan (GMB)

Selanjutnya kita akan membahas gerak melingkar beraturan atau GLB Adapun ciri-ciri GLB adalah sebagai berikut lintasannya berbentuk lingkaran dalam selang waktu yang sama besar posisi sudutnya sama besar kecepatan linear tetap tapi arahnya berubah besar dan arah kecepatan sudutnya tetap besar dan arah percepatan sentripetal nya tetap besar percepatan tangensialnya = 0 besar percepatan sudutnya sama dengan nol dan yang terakhir besar percepatan total = percepatan sentripetal.

contoh rumus persamaan GMB

Gerak Melingkar Berubah Beraturan (GMBB)

Berikutnya gerak melingkar berubah beraturan atau GLBB ciri-cirinya lintasannya berbentuk lingkaran dalam selang waktu yang sama besar posisi sudutnya berbeda besar dan arah kecepatan linearnya berubah besar dan arah kecepatan sudutnya berubah besar percepatan sentripetalnya berubah tetapi arahnya tetap besar percepatan tangensial nya tetap tapi arahnya berubah besar dan arah percepatan sudutnya tetap dan terakhir besar percepatan total adalah resultan vektor percepatan sentripetal dengan percepatan tangensial.

Nah berikut persamaan yang digunakan pada gerak melingkar berubah beraturan Omega 0 kecepatan sudut awal dan omega t kecepatan sudut akhir dalam radian per sekon Alfa percepatan sudut satuannya Radian per sekon kuadrat Teta posisi sudut dalam radian t adalah waktu satuannya sekon percepatan tangensial as percepatan sentripetal a total percepatan total dalam meter per sekon kuadrat.

contoh rumus persamaan GMBB

Hubungan Roda Roda Sepusat

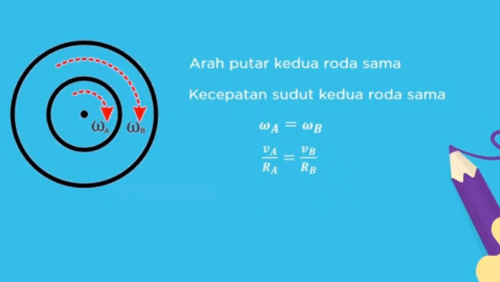
Sekarang kita akan membahas aplikasi yang terkait dengan gerak melingkar pada roda yang pertama hubungan roda-roda sepusat yang dimaksud roda-roda sepusat adalah 2 roda atau lebih yang berporos sama dan saling menyatu apabila roda roda sepusat diputar dalam selang waktu T maka kedua roda menempuh sudut pusat yang sama sehingga kecepatan sudut pada kedua roda sama dalam hal ini berlaku persamaan Omega a = Omega B sehingga ap = Rb

Hubungan Roda Roda Bersinggungan

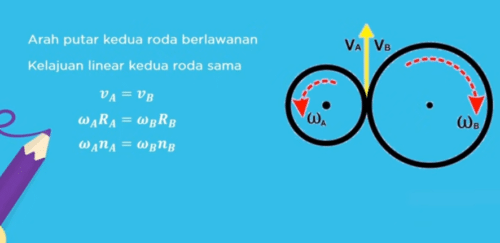
Yang kedua hubungan roda-roda bersinggungan pada roda roda yang saling bersinggungan arah putar ke dua roda berlawanan dan kelajuan liniernya sama Pa = PB sehingga A = Omega BRB salah satu contoh roda roda bersinggungan yaitu pada roda gigi mesin oleh karena ukuran gigi roda besar dan kecil sama roda yang lebih besar memiliki gigi lebih banyak jika banyak gigi untuk tiap roda dilambangkan dengan n maka hubungan roda gigi yang bersinggungan berlaku persamaan Omega n a = Omega Bnb

Hubungan Roda Roda Setali

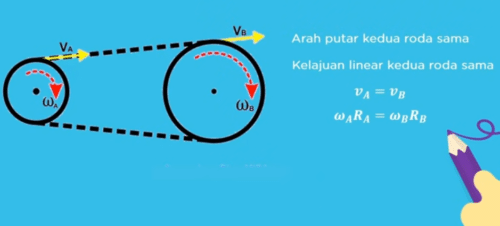
Yang terakhir hubungan roda-roda sekali roda roda yang dihubungkan dengan tali memiliki arah Putar dan laju linier yang sama Dalam keadaan ini berlaku persamaan Va = VB Omega a r a = Omega b Rb bisa dimengerti a teman-teman.

Oke jadi itu saja pembahasan seputar gerak melingkar, semoga mudah di pahami ya temen-temen.