Logika Matematika Ingkaran Konjungsi Disjungsi Implikasi dan Biimplikasi – Hai adik-adik ini kali kalian telah duduk di kelas 11 SMA, dan kita akan membahas info mengenai pelajaran matematika mengenai logika matematika. Apa sih logika matematika itu?
Penjelasan dari Logika matematika ialah ketentuan pengambilan satu simpulan yang benar lewat pertimbangan yang rasional. Dasar logika matematika ialah negasi, konjungsi, disjungsi, biimplikasi, dan implikasi. Janganlah bingung ya adik-adik hehe
di artikel ini kita langsung akan membahasnya satu-satu agar kalian lebih memahami lagi. Jadi yakinkan kalian membaca artikelnya sampai habis agar lebih pahami mengenai pembahasan materi ini. Selamat membaca ya adik-adik.

Pembahasan Materi Ingkaran, Konjungsi, Disjungsi, Implikasi dan Biimplikasi
Ingkaran atau Negasi (~)
Dari sebuah pengakuan, kita bisa membuat pengakuan baru berbentuk ingkaran atau negasi, yaitu penyanggahan atas pengakuan tadi. Agar semakin pahami ini, lihat tabel kebenaran ingkaran berikut ini:
Info:
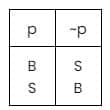
B = pernyataan bernilai benar
S = pernyataan bernilai salah
Maknanya, bila satu pertanyaan (p) betul, karena itu ingkaran (q) akan berharga salah. Begitupun sebaliknya. Nach, negasi ini disimbolkan dengan simbol garis semacam ini: ~
Contoh negasi dalam matematika yakni sebagai berikut:
p: Besi memuai bila dipanaskan (pengakuan berharga betul)
~p: Besi tidak memuai bila dipanaskan (pengakuan berharga salah).
Contoh lain:
p: Semua unggas ialah burung.
~p: Ada unggas yang bukan burung.
Bagaimaan telah pahami sampai sini adik-adik? Jika langsung ke pembahasan lain. Dalam pengetahuan matematika, ada 4 jenis pernyataan majemuk, yakni konjungsi, disjungsi, biimplikasi, dan implikasi. Yok, kita ulas satu demi satu!
Konjungsi (∧)
Konjungsi ialah pengakuan majemuk dalam kata hubung “dan “.Hingga, notasi “p ∧ q” dibaca “p dan q “.Berikut tabel nilai kebenaran konjungsi.
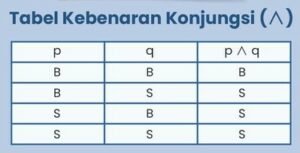
Info :
p = pernyataan 1
q = pernyataan 2
p ∧ q = p dan q
B = Benar
S = Salah
Dari tabel di atas, kita bisa menyaksikan jika konjungsi cuma akan betul bila ke-2 pengakuan (p dan q) betul.
Contoh:
p: 3 ialah bilangan sempurna (pengakuan berharga betul)
q: 3 ialah bilangan ganjil (pengakuan berharga betul)
p ∧ q: 3 ialah bilangan sempurna dan ganjil (pengakuan berharga betul)
Disjungsi (∨)
Disjungsi ialah pengakuan majemuk dalam kata hubung “atau “.Hingga notasi “p ∨ q” dibaca “p atau q “.Berikut tabel nilai kebenaran disjungsi.
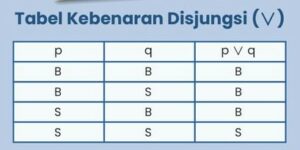
Info :
p = pengakuan 1
q = pengakuan 2
p ∨ q = p atau q
B = Betul
S = Salah
Bila kita saksikan pada tabel kebenaran, disjungsi cuma salah bila ke-2 pengakuan (p dan q) salah.
Contoh:
p: Paus ialah mamalia (pengakuan berharga betul)
q: Paus ialah herbivora (pengakuan berharga salah)
p ∨ q: Paus ialah mamalia atau herbivora (pengakuan berharga betul)
Implikasi (⇒)
Implikasi ialah pengakuan majemuk dalam kata hubung “jika… maka…” Hingga notasi dari “p ⇒ q” dibaca “Bila p, karena itu q “.Adapun tabel nilai kebenaran dari implikasi yakni sebagai berikut.
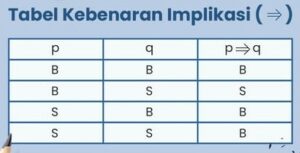
Info :
p = pengakuan 1
q = pengakuan 2
p ⇒ q = bila p karena itu q
B = Betul
S = Salah
Dari tabel kelihatan jika implikasi cuma berharga salah bila anteseden (p) betul, dan konsisten (q) salah.
Contoh:
p: Andi belajar dengan program ruangguru. (pengakuan berharga betul)
q: Andi bisa belajar dalam mana saja. (pengakuan berharga betul)
p ⇒ q: Bila Andi belajar dengan program ruangguru, karena itu Andi bisa belajar darimanakah saja (pengakuan berharga betul)
Biimplikasi (⇔)
Biimplikasi ialah pengakuan majemuk dalam kata hubung “… bila dan cuma bila “.Hingga, notasi dari “p ⇔ q” akan dibaca “p bila dan cuma bila q “.Adapun tabel nilai kebenaran dari biimplikasi yakni sebagai berikut.
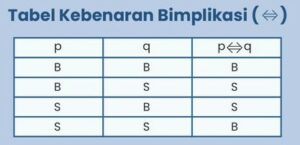
Info :
p = pengakuan 1
q = pengakuan 2
p ⇔ q = bila p dan cuma bila q
B = Betul
S = Salah
Dari tabel kebenaran itu, bisa kita perhatikan jika biimplikasi akan berharga betul bila karena dan mengakibatkan (pengakuan p dan q) berharga sama. Baik itu sama betul, atau sama salah.
Contoh:
p: 30 x 2 = 60 (pengakuan berharga betul)
q: 60 ialah bilangan ganjil (pengakuan berharga salah)
p ⇔ q: 30 x 2 = 60 bila dan cuma bila 60 ialah bilangan ganjil (pengakuan berharga salah).
Nach tersebut pembahasan berkenaan materi Logika Matematika Ingkaran, Konjungsi, Disjungsi, Implikasi dan Biimplikasi yang sukses kami rangkumkan dan kami suguhkan ke kalian semua. mudah-mudahan info ini berguna menambahkan pengetahuan kalian dan menuntaskan beberapa tugas kalian.
Terima kasih buat ayah bunda telah pilih situs website kami sebagai tutorial belajar anak-anak kalain. Untuk membaca materi yang lain dapat disaksikan langsung di kolom penelusuran karena kami menyuguhkan dimulai dari SD sampai perguruan tinggi.
baca juga :

